Donc, pour réaliser la première volonté dûe au premier Avril, on va faire un concours !
Mais ce concours n'est pas comme les autres !
C'est un concours à partir d'un exercice de mathématiques, sur les probabilités.
La règle est simple, à partir de l'énoncé, vous devez construire un arbre pondéré et répondre aux questions à l'aide de tout ce que vous avez sous la main.
Les prix :
1ère place : Un dessin au choix + lettre envoyée à votre adresse + Votre arbre pondéré publié avec un lien vers le blog.
Remporté par Tonin-de-jardin
2ème place : Croquis au choix + lien vers votre blog
Remporté par Axioule
Juste parce qu'il m'a bien fait rire ^^
3ème place : un lien vers votre blog
L'énoncé est très inspiré du cours de mon prof de maths =3
Mais c'est dans l'ambiance du blog et ça plaira bien aux geeks.
Terminé ! ♥
Dans un jeu électronique, Mishu combat un monstre. La machine choisit le monstre M1 avec une probabilité égale à 0,3 ; le monstre M2 avec une probabilité égale à 0,5 et le monstre M3 avec une probabilité égale à 0,2.
Si Mishu combat M1, la probabilité qu'elle gagne est de 0,4 ; si elle combat M2, la probabilité qu'elle gagne est égale à 0,3 et si elle combat M3 la probabilité qu'elle gagne est de 0,7.
Soit G l'événement "Mishu gagne le combat" et soient M1,M2,M3 les événements "la machine choisit le monstre M1/M2/M3"
Calculer la probabilité qu'elle gagne le combat.
Données : Utilisation de l'arbre pondéré - formule des probabilités totales - Probabilités conditionnelles - Pm1(G)
Petite aide :
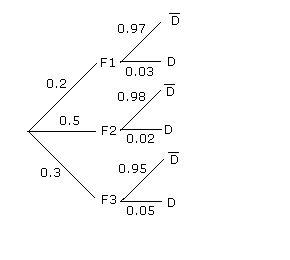
Remplacer les F par M, les données, et D par G.
Ensuite, sachez que pour calculer Pm1(G) = P(M1) x P(G) (ça se dit : probabilité de l'événement G sachant que M1 est réalisé)
Exemple : Pf2(D) = P(F2) x P(D) = 0.5 x 0.02 = 0.01
De plus, la loi des probabibilités totales est :

Avec le sorte de 3 à l'envers correspond à "somme".
C'est à dire :
P(A) = P(A|B1) x P(B1) + P(A|B2) x P(B2) + ... + P(A|Bn) x P(Bn)
Mais ce concours n'est pas comme les autres !
C'est un concours à partir d'un exercice de mathématiques, sur les probabilités.
La règle est simple, à partir de l'énoncé, vous devez construire un arbre pondéré et répondre aux questions à l'aide de tout ce que vous avez sous la main.
Les prix :
1ère place : Un dessin au choix + lettre envoyée à votre adresse + Votre arbre pondéré publié avec un lien vers le blog.
Remporté par Tonin-de-jardin
2ème place : Croquis au choix + lien vers votre blog
Remporté par Axioule
Juste parce qu'il m'a bien fait rire ^^
3ème place : un lien vers votre blog
L'énoncé est très inspiré du cours de mon prof de maths =3
Mais c'est dans l'ambiance du blog et ça plaira bien aux geeks.
Terminé ! ♥
Dans un jeu électronique, Mishu combat un monstre. La machine choisit le monstre M1 avec une probabilité égale à 0,3 ; le monstre M2 avec une probabilité égale à 0,5 et le monstre M3 avec une probabilité égale à 0,2.
Si Mishu combat M1, la probabilité qu'elle gagne est de 0,4 ; si elle combat M2, la probabilité qu'elle gagne est égale à 0,3 et si elle combat M3 la probabilité qu'elle gagne est de 0,7.
Soit G l'événement "Mishu gagne le combat" et soient M1,M2,M3 les événements "la machine choisit le monstre M1/M2/M3"
Calculer la probabilité qu'elle gagne le combat.
Données : Utilisation de l'arbre pondéré - formule des probabilités totales - Probabilités conditionnelles - Pm1(G)
Petite aide :

Remplacer les F par M, les données, et D par G.
Ensuite, sachez que pour calculer Pm1(G) = P(M1) x P(G) (ça se dit : probabilité de l'événement G sachant que M1 est réalisé)
Exemple : Pf2(D) = P(F2) x P(D) = 0.5 x 0.02 = 0.01
De plus, la loi des probabibilités totales est :

Avec le sorte de 3 à l'envers correspond à "somme".
C'est à dire :
P(A) = P(A|B1) x P(B1) + P(A|B2) x P(B2) + ... + P(A|Bn) x P(Bn)
